딥러닝에 있어서 가장 기본적인 두 가지 원리가 있습니다.
바로 선형회귀랑 로지스틱 회귀입니다.
그중 선형회귀에 대해 알아봅시다.
선형회귀란 독립변수 x를 사용해 종속변수 y의 움직임을 예측하고 설명하는 작업입니다.
성적을 예시로 들어봅시다. 공부한 시간에 따라 성적이 다르다고 가정할 때 성적이 종속변수 y 시간이 독립변수 x가 됩니다. 즉 몇 시간 공부하면 어느 정도 성적이 나오나 이런 예측을 하는 작업을 선형회귀라고 합니다.
여기서 시간만 주어진다면 단순 선형회귀, 시간이외에 사교육비 지출 및 교재비 등등 여러 독립변수가 추가되면 다중 선형회귀라고 합니다.
먼저 단순선형회귀를 살펴봅시다.
다음과 같은 데이터가 있다고 가정해봅시다.
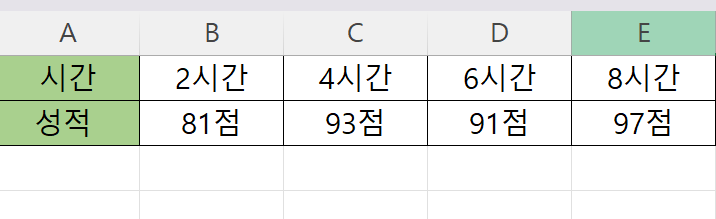
시간을 X라고 하고 성적을 Y라고 하면
$$ X = {2,4,6,8} $$
$$ Y = {81,93,91,97} $$
이렇게 나옵니다.
이걸 점 그래프로 나타내 봅시다.

선형 회귀는 이점들의 특징을 잘 나타내는 선을 그리는 과정과 일치합니다. 이 데이터의 특징을 담은 선은 일차함수와 일치합니다. 그렇다면 일차함수는 다음과 같이 표현이 가능합니다.
$$ y = ax + b $$
x는 독립변수이고 y는 종속변수입니다. 하지만 정확한 값을 알아내기 위해서는 a와 b의 값을 알아야 됩니다.
최소제곱법
이제 이 점들의 특징을 가장 잘나타내는 선을 그리면 됩니다. 일차함수로 말하자면 정확한 기울기 a와 절편 b를 알아야 됩니다. 여기서 최소제곱법 공식을 적용하면 a의 값과 b의 값을 구할 수 있습니다.
주어진 데이터를 바탕으로 a를 구하면
$$ a = \frac{(x - x 평균)(y - y평균)의 합}{(x-x평균)^2 의합} $$입니다.
이게 최소제곱법 공식입니다. 이제 값을다 대입해 봅시다.
x의 평균 = (2 + 4 + 6 + 8) / 4 = 5
y의 평균 = (81 + 93 + 91 + 97) / 4 = 90.5
이식을 최소제곱법 공식에 대입해봅시다. 그럼 2.3이 나옵니다.
이제 b를 구해봅시다.
$$ b = y의 평균 - (x의 평균 X 기울기 a) $$
값을 다 대입해보면 79가 나옵니다.
그러면 일차함수는
$$ y = 2.3x + 79 $$ 가 나옵니다.
이 일차함수를 그래프로 나타내면

이게 바로 오차가 가장 적은 주어진 좌표의 특성을 가장 잘 나타내는 직선입니다.
다음은 이걸 코랩과 파이썬으로 구현해 봅시다.
'Coding > AI' 카테고리의 다른 글
| 평균제곱오차란 무엇인가 (0) | 2023.09.27 |
|---|---|
| 코랩 파이썬으로 구현하는 최소제곱법 (0) | 2023.09.26 |
| 딥러닝을 위한 기초수학2 (0) | 2023.09.26 |
| 딥러닝을 위한 기초수학 (0) | 2023.09.25 |
| 구글 코랩 실행하기 (0) | 2023.09.25 |




