안녕하세요
평균제곱오차를 보면 임의의 선을 하나 긋습니다. 여기서 주어진 데이터에 비해 경사가 높은 선을 그으면 오차가 커집니다. 반대로 경사가 너무 낮은 선을 그어도 오차가 커집니다.


평균제곱오차 공식을 다시 살펴보죠
$$ 평균제곱오차 = \frac{1}{n}\sum{(y-y')^2} $$
여기서 y는 실제값 y'은 예측값 이었습니다.
식을 보면 제곱이 나오는걸 확인할수있습니다. 즉 오차와 기울기에 관계는 이차함수라는걸 알수있습니다.
그래프로 나타내면 다음과 같습니다.

여기서 오차가 제일 작은 부분은 점으로 찍힌 제일 밑으로 볼록한 부분이죠
이부분이 바로 "미분 값이 0인 지점" 입니다. 즉 순간변화율이 0인부분인거죠
이부분을 "하강"하면서 미분을 해줍니다. 그러면서 미분이 0인 부분을 찾으면 됩니다. 이게 경사하강법입니다.

여기서 학습률의 개념이 나옵니다. 첫번째 점을 찍었을때 미분을 했다고 칩시다. 그리고 그다음 미분을 합니다. 이때 얼마만큼 떨어져서 미분할까 이게 학습률입니다. 학습률이 높을수록 더 멀리 미분을 하게 되고 적을수록 더 적게 넘어가서 미분을 하게 됩니다.


이걸 조절하는게 굉장히 중요합니다. 학습률이 높을수록 속도는 빨라집니다만 오차가 더 커질수 있고 학습률이 너무 작으면 수렴속도가 굉장히 느려지고 수렴을 못하고 지역 최소값에 빠질수있습니다. 또한 학습이 중단될수가 있죠
이 경사하강법을 파이썬으로 나타내봅시다.
먼저 평균제곱오차식을 다시 가져와 봅시다.
$$ 평균제곱오차 = \frac{1}{n}\sum{(y-y')^2} $$
여기서 y'은 예측선 즉 가설로 세운 선의 y축 값을 말합니다.y = ax + b 여기서 x대신 가설로 세운 x'을 넣은것이죠
y' 대신 ax'+b을 넣어봅시다. 그러면
$$ 평균제곱오차 = \frac{1}{n}\sum{(y-(ax'+b))^2} $$
여기서 a와 b값을 구해야됩니다. 그러기 위해선 a와 b로 각각 편미분을 해야됩니다.
$$ a로 편미분한 결과 = \frac {2}{n}\sum-x'(y-(ax'+b)) $$
$$ b로 편미분한 결과 = \frac{2}{n}\sum-(y - (ax'+b)) $$
이제 이걸 파이썬으로 옮겨 봅시다.
먼저 넘파이랑 matplotlib.pyplot를 임포트 해줍시다.
그런다음 넘파이 배열을 설정해주고 그래프를 출력 해줍시다.


그다음 기울기 a와 절편 b의 값을 초기화해주고
학습률 및 몇번 반복할지 에포크를 정해줍시다. 그다음 x값이 총 몇개인지 세줍니다.

그다음 경사하강법을 구현해줍니다.
먼저 반복문을 통해 에포크 수 만큼 반복을 해줍니다.
예측값을 구하고
그 예측값과 실제값에 대한 오차를 구해줍니다.
그리고 아까 a와 b로 각각 편미분한 식을 구현해주고
이 편미분한 식에 오차와 x값을 넣어줍니다. 그리고 학습률을 곱해 기존에 a와 b값을 각각 업데이트 해줍니다. 마지막으로 이값을 그래프로 출력해줍니다.

처음에 나왔던 그래프창을 닫아주면 새로운 선이 그어진 그래프를 확인하실수있습니다.
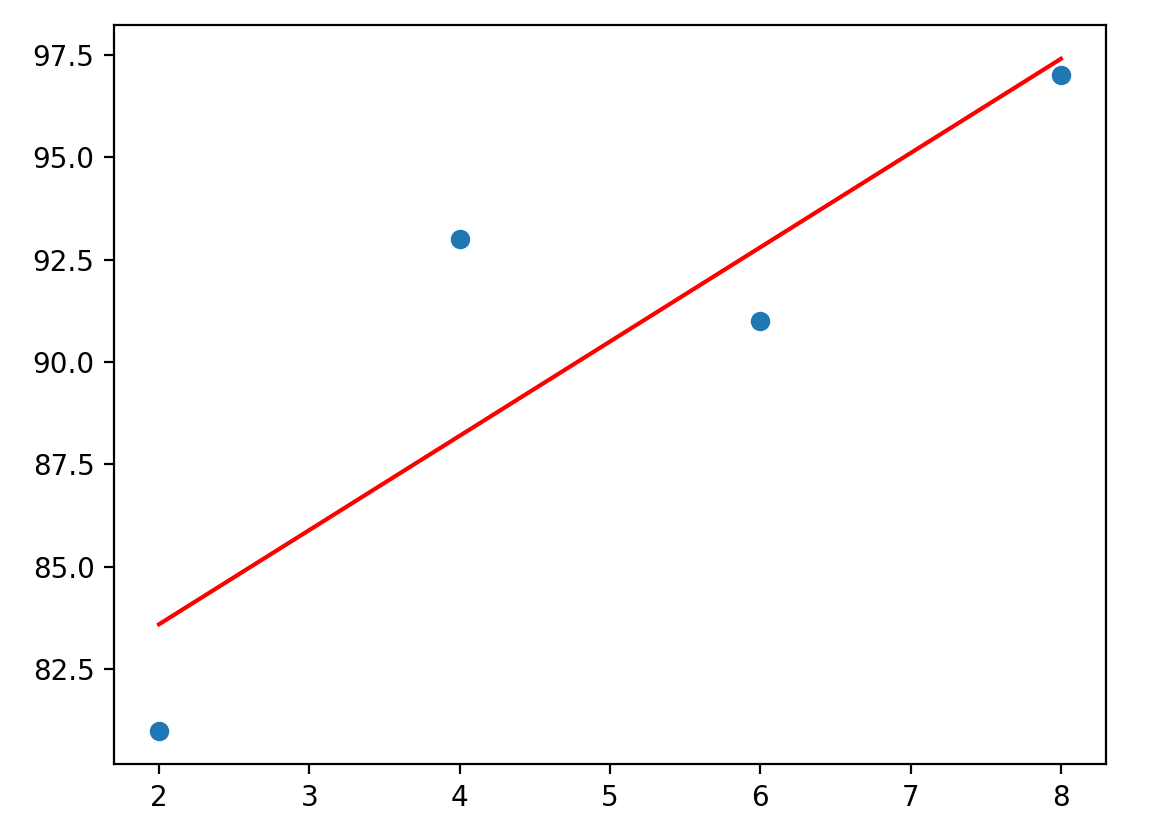
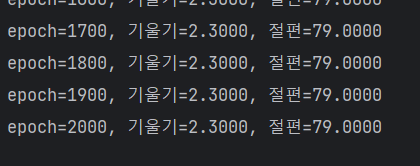
기울기와 절편은 아래와 같이 확인할수있습니다.
'Coding > AI' 카테고리의 다른 글
| Tensorflow로 선형회귀를 구현해보자 (0) | 2023.10.08 |
|---|---|
| 다중선형회귀란 무엇인가 (0) | 2023.10.07 |
| 파이썬으로 구현하는 평균 제곱 오차 (0) | 2023.09.27 |
| 평균제곱오차란 무엇인가 (0) | 2023.09.27 |
| 코랩 파이썬으로 구현하는 최소제곱법 (0) | 2023.09.26 |




